VB.Net Program to Find a Function Minimum

Using the Grid Search Method

by Namir Shammas

The following program calculates the minimum point of a multi-variable function using the grid search method. This method performs a multi-dimensional grid search. The grid is defined by a multiple dimensions. Each dimension has a range of values. Each range is divided into a set of equal-value intervals. The multi-dimensional grid has a centroid which locates the optimum point. The search involves multiple passes. In each pass, the method local a node (point of intersection) with the least function value. This node becomes the new centroid and builds a smaller grid around it. Successive passes end up shrinking the multidimensional grid around the optimum.

Click here to download a ZIP file containing the project files for this program.

The program prompts you to either use the predefined default input values or to enter the following for each variable (i.e. dimension):

1. The values that define the lower and upper limits of a search range for a variable,

2. The number of divisions for a range.

3. The minimum range value, used to determine when to stop searching..

The program also asks you to enter the function tolerance. The program uses this value to possible stop iterating when successive best function values are close enough.

In case you choose the default input values, the program displays these values and proceeds to find the optimum point. In the case you select being prompted, the program displays the name of each input variable along with its default value. You can then either enter a new value or simply press Enter to use the default value. This approach allows you to quickly and efficiently change only a few input values if you so desire.

The program displays the following final results:

1. The coordinates of the minimum point.

2. The minimum function value.

3. The number of iterations

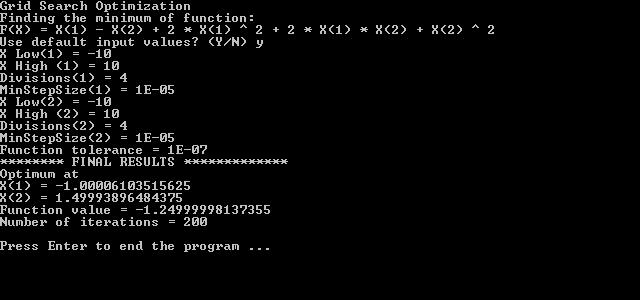
Here is a sample session to find the minimum of function:

f(x) = x1 - x2 + 2 * x1 ^ 2 + 2 * x1 * x2 + x2 ^ 2

Using, for each variable, the range of (-10, 10), initial range divisions of 4, minimum step size of 1e-5. The solution also uses a function tolerance of 1e-7. Here is the sample console screen:

Here is the listing for the main module. The module contains several test functions:

Module Module1

  Sub Main()
    Dim nNumVars As Integer = 2
    Dim fX() As Double = {0, 0}
    Dim fParam() As Double = {0, 0}
    Dim fXLo() As Double = {-10, -10}
    Dim fXHi() As Double = {10, 10}
    Dim nNumDiv() As Integer = {4, 4}
    Dim fMinDeltaX() As Double = {0.00001, 0.00001}
    Dim nIter As Integer = 0
    Dim fEpsFx As Double = 0.0000001
    Dim I As Integer
    Dim fBestF
    Dim sAnswer As String
    Dim oOpt As CGridSearch
    Dim MyFx As MyFxDelegate = AddressOf Fx3
    Dim SayFx As SayFxDelegate = AddressOf SayFx3

    oOpt = New CGridSearch

    Console.WriteLine("Grid Search Optimization")
    Console.WriteLine("Finding the minimum of function:")
    Console.WriteLine(SayFx())
    Console.Write("Use default input values? (Y/N) ")
    sAnswer = Console.ReadLine()
    If sAnswer.ToUpper() = "Y" Then
      For I = 0 To nNumVars - 1
        Console.WriteLine("X Low({0}) = {1}", I + 1, fXLo(I))
        Console.WriteLine("X High ({0}) = {1}", I + 1, fXHi(I))
        Console.WriteLine("Divisions({0}) = {1}", I + 1, nNumDiv(I))
        Console.WriteLine("MinStepSize({0}) = {1}", I + 1, fMinDeltaX(I))
      Next
      Console.WriteLine("Function tolerance = {0}", fEpsFx)
    Else
      For I = 0 To nNumVars - 1
        fXLo(I) = GetIndexedDblInput("X low", I + 1, fXLo(I))
        fXHi(I) = GetIndexedDblInput("X high", I + 1, fXHi(I))
        nNumDiv(I) = GetIndexedIntInput("Number of divisions", I + 1, nNumDiv(I))
        fMinDeltaX(I) = GetIndexedDblInput("Minimum step size", I + 1, fMinDeltaX(I))
      Next
      fEpsFx = GetDblInput("Function tolerance", fEpsFx)
    End If

    Console.WriteLine("******** FINAL RESULTS *************")
    fBestF = oOpt.CalcOptim(nNumVars, fX, fParam, fXLo, fXHi, nNumDiv, fMinDeltaX, fEpsFx, nIter, MyFx)
    Console.WriteLine("Optimum at")
    For I = 0 To nNumVars - 1
      Console.WriteLine("X({0}) = {1}", I + 1, fX(I))
    Next
    Console.WriteLine("Function value = {0}", fBestF)
    Console.WriteLine("Number of iterations = {0}", nIter)
    Console.WriteLine()
    Console.Write("Press Enter to end the program ...")
    Console.ReadLine()
  End Sub

  Function GetDblInput(ByVal sPrompt As String, ByVal fDefInput As Double) As Double
    Dim sInput As String

    Console.Write("{0}? ({1}): ", sPrompt, fDefInput)
    sInput = Console.ReadLine()
    If sInput.Trim().Length > 0 Then
      Return Double.Parse(sInput)
    Else
      Return fDefInput
    End If
  End Function

  Function GetIntInput(ByVal sPrompt As String, ByVal nDefInput As Integer) As Integer
    Dim sInput As String

    Console.Write("{0}? ({1}): ", sPrompt, nDefInput)
    sInput = Console.ReadLine()
    If sInput.Trim().Length > 0 Then
      Return Double.Parse(sInput)
    Else
      Return nDefInput
    End If
  End Function

  Function GetIndexedDblInput(ByVal sPrompt As String, ByVal nIndex As Integer, ByVal fDefInput As Double) As Double
    Dim sInput As String

    Console.Write("{0}({1})? ({2}): ", sPrompt, nIndex, fDefInput)
    sInput = Console.ReadLine()
    If sInput.Trim().Length > 0 Then
      Return Double.Parse(sInput)
    Else
      Return fDefInput
    End If
  End Function

  Function GetIndexedIntInput(ByVal sPrompt As String, ByVal nIndex As Integer, ByVal nDefInput As Integer) As Integer
    Dim sInput As String

    Console.Write("{0}({1})? ({2}): ", sPrompt, nIndex, nDefInput)
    sInput = Console.ReadLine()
    If sInput.Trim().Length > 0 Then
      Return Double.Parse(sInput)
    Else
      Return nDefInput
    End If
  End Function

  Function SayFx1() As String
    Return "F(X) = 10 + (X(1) - 2) ^ 2 + (X(2) + 5) ^ 2"
  End Function

  Function Fx1(ByVal N As Integer, ByRef X() As Double, ByRef fParam() As Double) As Double
    Return 10 + (X(0) - 2) ^ 2 + (X(1) + 5) ^ 2
  End Function

  Function SayFx2() As String
    Return "F(X) = 100 * (X(1) - X(2) ^ 2) ^ 2 + (X(2) - 1) ^ 2"
  End Function

  Function Fx2(ByVal N As Integer, ByRef X() As Double, ByRef fParam() As Double) As Double
    Return 100 * (X(0) - X(1) ^ 2) ^ 2 + (X(1) - 1) ^ 2
  End Function

  Function SayFx3() As String
    Return "F(X) = X(1) - X(2) + 2 * X(1) ^ 2 + 2 * X(1) * X(2) + X(2) ^ 2"
  End Function

  Function Fx3(ByVal N As Integer, ByRef X() As Double, ByRef fParam() As Double) As Double
    Return X(0) - X(1) + 2 * X(0) ^ 2 + 2 * X(0) * X(1) + X(1) ^ 2
  End Function

End Module

Notice that the user-defined functions have accompanying helper functions to display the mathematical expression of the function being optimized. For example, function Fx1 has the helper function SayFx1 to list the function optimized in Fx1. Please observe the following rules::

When you add new user-defined functions to optimize, you must also add an accompanying helper function that states the function mathematical make up.
When you edit an existing user-defined functions to optimize, you must also edit its accompanying helper function to reflect the changes you make in the function mathematical make up
When you select a new user-defined function you must alter both variables MyFx, and SayFx to specify the new function and its accompanying helper function.

The program uses the following class to optimize the objective function:

Public Delegate Function MyFxDelegate(ByVal nNumVars As Integer, ByRef fX() As Double, ByRef fParam() As Double) As Double
Public Delegate Function SayFxDelegate() As String

Public Class CGridSearch

  Public Function CalcOptim(ByVal nNumVars As Integer, ByRef fXCenter() As Double, ByRef fParam() As Double, _
                  ByRef fXLo() As Double, ByRef fXHi() As Double, ByRef nNumDiv() As Integer, _
                  ByRef fMinDeltaX() As Double, ByVal fEpsFx As Double, ByRef nIter As Integer, _
                  ByVal MyFx As MyFxDelegate) As Double
    Dim fDeltaX(), fX(), fBestX() As Double
    Dim F, fBestF, fLastBestF As Double
    Dim I As Integer
    Dim bGoOn As Boolean

    ReDim fDeltaX(nNumVars), fX(nNumVars), fBestX(nNumVars)

    For I = 0 To nNumVars - 1
      fXCenter(I) = (fXLo(I) + fXHi(I)) / 2
      fBestX(I) = fXCenter(I)
      fDeltaX(I) = (fXHi(I) - fXLo(I)) / nNumDiv(I)
      fX(I) = fXLo(I)
    Next

    ' calculate and display function value at initial point
    fBestF = MyFx(nNumVars, fXCenter, fParam)
    If fBestF > 0 Then
      fLastBestF = 100 + fBestF
    Else
      fLastBestF = 100 - fBestF
    End If

    nIter = 0
    Do

      Do
        nIter += 1

        F = MyFx(nNumVars, fX, fParam)
        If F < fBestF Then
          fLastBestF = fBestF
          fBestF = F
          For I = 0 To nNumVars - 1
            fBestX(I) = fX(I)
          Next I
        End If

        '*****************************************************
        ' The next For loop implements a programming tricks
        ' that simulated nested loops using just one For loop
        '*****************************************************
        ' search next grid node
        For I = 0 To nNumVars - 1
          If fX(I) >= fXHi(I) Then
            If I < (nNumVars - 1) Then
              fX(I) = fXLo(I)
            Else
              Exit Do
            End If
          Else
            fX(I) += fDeltaX(I)
            Exit For
          End If
        Next I
      Loop

      For I = 0 To nNumVars - 1
        fXCenter(I) = fBestX(I)
        fDeltaX(I) = fDeltaX(I) / nNumDiv(I)
        fXLo(I) = fXCenter(I) - fDeltaX(I) * nNumDiv(I) / 2
        fXHi(I) = fXCenter(I) + fDeltaX(I) * nNumDiv(I) / 2
        fX(I) = fXLo(I) ' set initial fX
      Next I

      ' fBestF = MyFx(XCenter, N)
      bGoOn = False
      For I = 0 To nNumVars - 1
        If fDeltaX(I) > fMinDeltaX(I) Then bGoOn = True
      Next I

      bGoOn = bGoOn And (Math.Abs(fBestF - fLastBestF) > fEpsFx)

    Loop While bGoOn

    Return fBestF

  End Function
End Class

BACK