VB.Net Program to Find a Function Minimum

Using a Direct Search Method

by Namir Shammas

The following program calculates the minimum point of a multi-variable function using direct search method.

Click here to download a ZIP file containing the project files for this program.

The pseudo-code for this algorithm is:

Given

The number of variables N
The array of initial values X
The array of initial search steps S
The array of minimum search steps M

Method

F0 = F(X)
For I = 1 to N
Let X0 = X(I)
X(I) = X(I) + S(I)
If F(X) < F0 then go to step 10
Let X(I) = X0 - S(I)
If F(X) < F0 then go to step 11
X(I) = X0
If S(I) <= M(I) then Let S(I) = S(I) / 10
Go to step 12
F0 = F(X)
Next I
Let S0 = 0
For I = 1 to N
If S(I) >= M(I) then S0 = 1
Next I
If S0 > 0 Then go to step 2
Display array X()

The program prompts you to either use the predefined default input values or to enter the following for each variable:

1. Guess for the minimum point.

2. Initial search step value.

3. The minimum search step value.

In case you choose the default input values, the program displays these values and proceeds to find the optimum point. In the case you select being prompted, the program displays the name of each input variable along with its default value. You can then either enter a new value or simply press Enter to use the default value. This approach allows you to quickly and efficiently change only a few input values if you so desire.

The program displays the following results:

1. The coordinates of the minimum value.

2. The minimum function value.

3. The number of iterations

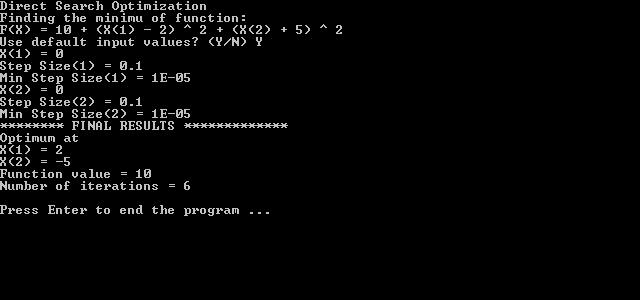
Here is a sample session to find the minimum of function:

f(x) = 10 + (x1-2)^2 + (x2+5)^2

Using initial values of 0, initial search steps of 0.1 for both variables, and minimum search steps of 1e-5 for both variables. Here is the sample console screen:

Here is the BASIC listing for the main module. The module contains several test functions:

Module Module1

  Sub Main()
    Dim nNumVars As Integer = 2
    Dim fX() As Double = {0, 0}
    Dim fParam() As Double = {0, 0}
    Dim fStepSize() As Double = {0.1, 0.1}
    Dim fMinStepSize() As Double = {0.00001, 0.00001}
    Dim nIter As Integer = 0
    Dim I As Integer
    Dim fBestF As Double
    Dim sAnswer As String
    Dim oOpt As CDirectSearch
    Dim MyFx As MyFxDelegate = AddressOf Fx1
    Dim SayFx As SayFxDelegate = AddressOf SayFx1

    oOpt = New CDirectSearch

    Console.WriteLine("Direct Search Optimization")
    Console.WriteLine("Finding the minimu of function:")
    Console.WriteLine(SayFx())
    Console.Write("Use default input values? (Y/N) ")
    sAnswer = Console.ReadLine()
    If sAnswer.ToUpper() = "Y" Then
      For I = 0 To nNumVars - 1
        Console.WriteLine("X({0}) = {1}", I + 1, fX(I))
        Console.WriteLine("Step Size({0}) = {1}", I + 1, fStepSize(I))
        Console.WriteLine("Min Step Size({0}) = {1}", I + 1, fMinStepSize(I))
      Next
    Else
      For I = 0 To nNumVars - 1
        fX(I) = GetIndexedDblInput("X", I + 1, fX(I))
        fStepSize(I) = GetIndexedDblInput("Initial step size(", I + 1, fStepSize(I))
        fMinStepSize(I) = GetIndexedDblInput("Minimum step size", I + 1, fMinStepSize(I))
      Next
    End If

    Console.WriteLine("******** FINAL RESULTS *************")
    fBestF = oOpt.DirectSearch(nNumVars, fX, fParam, fStepSize, fMinStepSize, nIter, MyFx)
    Console.WriteLine("Optimum at")
    For I = 0 To nNumVars - 1
      Console.WriteLine("X({0}) = {1}", I + 1, fX(I))
    Next
    Console.WriteLine("Function value = {0}", fBestF)
    Console.WriteLine("Number of iterations = {0}", nIter)
    Console.WriteLine()
    Console.Write("Press Enter to end the program ...")
    Console.ReadLine()
  End Sub

  Function GetDblInput(ByVal sPrompt As String, ByVal fDefInput As Double) As Double
    Dim sInput As String

    Console.Write("{0}? ({1}): ", sPrompt, fDefInput)
    sInput = Console.ReadLine()
    If sInput.Trim().Length > 0 Then
      Return Double.Parse(sInput)
    Else
      Return fDefInput
    End If
  End Function

  Function GetIndexedDblInput(ByVal sPrompt As String, ByVal nIndex As Integer, ByVal fDefInput As Double) As Double
    Dim sInput As String

    Console.Write("{0}({1})? ({2}): ", sPrompt, nIndex, fDefInput)
    sInput = Console.ReadLine()
    If sInput.Trim().Length > 0 Then
      Return Double.Parse(sInput)
    Else
      Return fDefInput
    End If
  End Function

  Function SayFx1() As String
    Return "F(X) = 10 + (X(1) - 2) ^ 2 + (X(2) + 5) ^ 2"
  End Function

  Function Fx1(ByVal N As Integer, ByRef X() As Double, ByRef fParam() As Double) As Double
    Return 10 + (X(0) - 2) ^ 2 + (X(1) + 5) ^ 2
  End Function

  Function SayFx2() As String
    Return "F(X) = 100 * (X(1) - X(2) ^ 2) ^ 2 + (X(2) - 1) ^ 2"
  End Function

  Function Fx2(ByVal N As Integer, ByRef X() As Double, ByRef fParam() As Double) As Double
    Return 100 * (X(0) - X(1) ^ 2) ^ 2 + (X(1) - 1) ^ 2
  End Function

  Function SayFx3() As String
    Return "F(X) = X(1) - X(2) + 2 * X(1) ^ 2 + 2 * X(1) * X(2) + X(2) ^ 2"
  End Function

  Function Fx3(ByVal N As Integer, ByRef X() As Double, ByRef fParam() As Double) As Double
    Return X(0) - X(1) + 2 * X(0) ^ 2 + 2 * X(0) * X(1) + X(1) ^ 2
  End Function

End Module

Notice that the user-defined functions have accompanying helper functions to display the mathematical expression of the function being optimized. For example, function Fx1 has the helper function SayFx1 to list the function optimized in Fx1. Please observe the following rules::

When you add new user-defined functions to optimize, you must also add an accompanying helper function that states the function mathematical make up.
When you edit an existing user-defined functions to optimize, you must also edit its accompanying helper function to reflect the changes you make in the function mathematical make up
When you select a new user-defined function you must alter both variables MyFx, and SayFx to specify the new function and its accompanying helper function.

The program uses the following class to optimize the objective function:

Public Delegate Function MyFxDelegate(ByVal nNumVars As Integer, ByRef fX() As Double, ByRef fParam() As Double) As Double
Public Delegate Function SayFxDelegate() As String

Public Class CDirectSearch

  Public Function DirectSearch(ByVal nNumVars As Integer, ByRef fX() As Double, ByRef fParam() As Double, _
                  ByRef fStepSize() As Double, ByRef fMinStepSize() As Double, ByRef nIter As Integer, _
                  ByVal MyFx As MyFxDelegate) As Double
    Const StepReduceFactor As Integer = 10

    Dim fBestF As Double
    Dim F, fXX As Double
    Dim I As Integer
    Dim bStop, bFound As Boolean

    fBestF = MyFx(nNumVars, fX, fParam)

    nIter = 0
    Do
      nIter = nIter + 1

      For I = 0 To nNumVars - 1
        bFound = False
        Do
          fXX = fX(I)
          fX(I) = fXX + fStepSize(I)
          F = MyFx(nNumVars, fX, fParam)
          If F < fBestF Then
            fBestF = F
            bFound = True
          Else
            fX(I) = fXX - fStepSize(I)
            F = MyFx(nNumVars, fX, fParam)
            If F < fBestF Then
              fBestF = F
              bFound = True
            Else
              fX(I) = fXX
              If Not bFound Then
                fStepSize(I) = fStepSize(I) / StepReduceFactor
              End If
              Exit Do
            End If
          End If
        Loop
      Next I

      bStop = True
      For I = 0 To nNumVars - 1
        If fStepSize(I) >= fMinStepSize(I) Then
          bStop = False
          Exit For
        End If
      Next I

    Loop Until bStop

    Return fBestF

  End Function
End Class

BACK