The following program uses the Marquardt method to find the minimum of a function.
The program prompts you to enter for each variable (i.e. dimension):
1. The gradient norm tolerance.
2. The maximum number of iterations.
3. The Alpha factor (a large value like 1E+4 is suitable).
4. The value for C1 and C2 factors (values for C1 = 0.1 and C2 = 10 are generally adequate)
5. The initial guesses for the optimum point for each variable.
6. The tolerance values for each variable.
The program displays the following final results:
1. The coordinates of the minimum point.
2. The minimum function value.
3. The number of iterations
The current code finds the minimum for the following function:
f(x1,x2) = x1 - x2 + 2 * x1 ^ 2 + 2 * x1 * x2 + x2 ^ 2
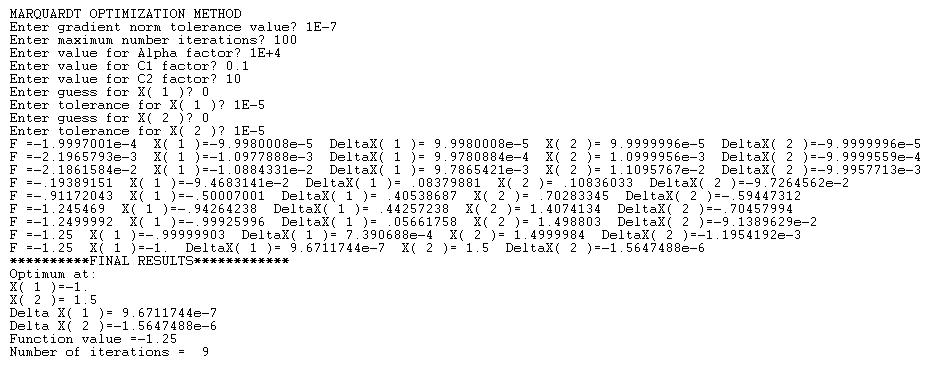
Here is a sample session to solve for the optimum of the above function:

Here is the BASIC listing:
! Marquardt's Method for Optimization
OPTION TYPO
OPTION NOLET
DECLARE NUMERIC MAX_VARS, ALPHA_MAX
DECLARE NUMERIC N, I, F1, F2, Lambda, Alpha, C1, C2
DECLARE NUMERIC EPSF, fNorm
DECLARE NUMERIC Iter, MaxIter, InnerLoopIter
DECLARE NUMERIC bStop, bOK, bTrue, bFalse, bStop2
Dim X(1), X2(1), g(1,1)
Dim Toler(1)
Dim DeltaX(1), J(1, 1)
Dim Iden(1,1), Iden2(1,1)
MAX_VARS = 2
bTrue = 1
bFalse = 0
ALPHA_MAX = 1E+100
SUB MyFx(X(), N, Res)
!Res = 100 * (X(1) ^ 2 - X(2)) ^ 2 + (1 - X(1)) ^ 2
Res = X(1) - X(2) + 2 * X(1) ^ 2 + 2 * X(1) * X(2) + X(2) ^ 2
END SUB
SUB MyFxEx(N,X(),DeltaX(), Lambda, funRes)
LOCAL I
Dim XX(1)
MAT REDIM XX(N)
For I = 1 To N
XX(I) = X(I) + Lambda * DeltaX(I)
Next I
CALL MyFx(XX, N, funRes)
END SUB
SUB LinSearch_DirectSearch(X(), N, Lambda, DeltaX(), boolRes)
LOCAL MAX_ITER, TOLER
LOCAL Iter, h, Diff, F0, Fp, Fm, Deriv1, Deriv2
MAX_ITER = 100
TOLER = 0.000001
boolRes = bTrue
Iter = 0
Do
Iter = Iter + 1
If Iter > MAX_ITER Then
boolRes = bFalse
Exit SUB
End If
h = 0.01 * (1 + Abs(Lambda))
CALL MyFxEx(N, X, DeltaX, Lambda, F0)
CALL MyFxEx(N, X, DeltaX, Lambda + h, Fp)
CALL MyFxEx(N, X, DeltaX, Lambda - h, Fm)
Deriv1 = (Fp - Fm) / 2 / h
Deriv2 = (Fp - 2 * F0 + Fm) / h ^ 2
If Deriv2 = 0 Then Exit SUB
Diff = Deriv1 / Deriv2
Lambda = Lambda - Diff
Loop Until Abs(Diff) < TOLER
END SUB
SUB FirstDeriv(N, X(), iVar, funRes)
LOCAL Xt, h, Fp, Fm
Xt = X(iVar)
h = 0.01 * (1 + Abs(Xt))
X(iVar) = Xt + h
CALL MyFx(X, N, Fp)
X(iVar) = Xt - h
CALL MyFx(X, N, Fm)
X(iVar) = Xt
funRes = (Fp - Fm) / 2 / h
END SUB
SUB SecondDeriv(N, X(), iVar, jVar, funRes)
LOCAL Xt, Yt,HX, HY,F0, Fp, Fm
LOCAL Fpp, Fmm, Fpm, Fmp
! calculate second derivative?
If iVar = jVar Then
CALL MyFx(X, N, F0)
Xt = X(iVar)
HX = 0.01 * (1 + Abs(Xt))
X(iVar) = Xt + HX
CALL MyFx(X, N, Fp)
X(iVar) = Xt - HX
CALL MyFx(X, N, Fm)
X(iVar) = Xt
funRes = (Fp - 2 * F0 + Fm) / HX ^ 2
Else
Xt = X(iVar)
Yt = X(jVar)
HX = 0.01 * (1 + Abs(Xt))
HY = 0.01 * (1 + Abs(Yt))
! calculate Fpp
X(iVar) = Xt + HX
X(jVar) = Yt + HY
CALL MyFx(X, N, Fpp)
! calculate Fmm
X(iVar) = Xt - HX
X(jVar) = Yt - HY
CALL MyFx(X, N, Fmm)
! calculate Fpm
X(iVar) = Xt + HX
X(jVar) = Yt - HY
CALL MyFx(X, N, Fpm)
! calculate Fmp
X(iVar) = Xt - HX
X(jVar) = Yt + HY
CALL MyFx(X, N, Fmp)
X(iVar) = Xt
X(jVar) = Yt
funRes = (Fpp - Fmp - Fpm + Fmm) / (4 * HX * HY)
End If
END SUB
SUB GetFirstDerives(N, X(), FirstDerivX(,))
LOCAL I
For I = 1 To N
CALL FirstDeriv(N, X, I, FirstDerivX(I,1))
Next I
END SUB
SUB GetSecondDerives(N, X(), SecondDerivX(,))
LOCAL I, J
For I = 1 To N
For J = 1 To N
CALL SecondDeriv(N, X, I, J, SecondDerivX(I, J))
Next J
Next I
END SUB
! Marquardt's Method for Optimization
N = MAX_VARS
MAT REDIM X(N), X2(N), g(N,1)
MAT REDIM Toler(N)
MAT REDIM DeltaX(N), J(N, N)
MAT REDIM Iden(N,N), Iden2(N,N)
PRINT "MARQUARDT OPTIMIZATION METHOD"
INPUT PROMPT "Enter gradient norm tolerance value? ": EPSF
INPUT PROMPT "Enter maximum number iterations? ": MaxIter
INPUT PROMPT "Enter value for Alpha factror? ": Alpha
INPUT PROMPT "Enter value for C1 factror? ": C1
INPUT PROMPT "Enter value for C2 factror? ": C2
For I = 1 To N
PRINT "Enter guess for X(";I;")";
INPUT X(I)
PRINT "Enter tolerance for X(";I;")";
INPUT Toler(I)
Next I
CALL MyFx(X, N, F2)
Iter = 0
Do
Iter = Iter + 1
If Iter > MaxIter Then
PRINT "Reached maximum iterations limit"
Exit Do
End If
! copy last Fx value
F1 = F2
CALL GetFirstDerives(N, X, g)
! test if gradient is shallow enough
fNorm = 0
For I = 1 To N
fNorm = fNorm + g(I,1)^2
Next I
fNorm = Sqr(fNorm)
If fNorm < EPSF Then Exit Do
! copy vector X
MAT X2 = X
! get matrix J
CALL GetSecondDerives(N, X, J)
! create identitty matrix
MAT Iden = IDN(N,N)
! Initializer inner loop
InnerLoopIter = 0
Do
InnerLoopIter = InnerLoopIter + 1
If InnerLoopIter > MaxIter Then Exit Do
MAT Iden2 = Alpha * Iden
MAT J = J + Iden2
MAT J = INV(J)
MAT g = J * g
For I = 1 To N
DeltaX(I) = g(I,1)
X(I) = X(I) - DeltaX(I)
Next I
CALL MyFx(X, N, F2)
PRINT "F =";F2;" ";
For I = 1 To N
PRINT "X(";I;")=";X(I);" DeltaX(";I;")=";DeltaX(I);" ";
Next I
PRINT
If F2 < F1 Then
Alpha = C1 * Alpha
bStop = bTrue
Else
Alpha = C2 * Alpha
MAT X = X2 ! objML.DuplicateVector X2, X ' restore array X
bStop = bFalse
If Alpha >= ALPHA_MAX Then
PRINT "**********SOLUTION FAILES************"
End If
End If
bStop2 = bTrue
For I = 1 To N
If Abs(DeltaX(I)) > Toler(I) Then
bStop2 = bFalse
Exit For
End If
Next I
Loop Until (bStop = bTrue) OR (bStop2 = bTrue)
If InnerLoopIter > MaxIter Then Exit Do
If Alpha >= ALPHA_MAX Then Exit Do
Loop Until bStop2 = bTrue
CALL MyFx(X, N, F2)
PRINT "**********FINAL RESULTS************"
PRINT "Optimum at:"
For I = 1 To N
PRINT "X(";I;")=";X(I)
Next I
For I = 1 To N
PRINT "Delta X(";I;")=";DeltaX(I)
Next I
PRINT "Function value ="; F2
PRINT "Number of iterations = ";Iter
END
Copyright (c) Namir Shammas. All rights reserved.