True BASIC Program to Find a Function Minimum

Using the Hooke-Jeeves Directional Search Method

by Namir Shammas

The following program calculates the minimum point of a multi-variable function using the Hooke-Jeeves directional search method.

The program prompts you to enter for each variable:

1. Guess for the minimum point.

2. Initial search step value.

3. The minimum search step value.

The program displays intermediate results to show the iteration progress and also the following final results:

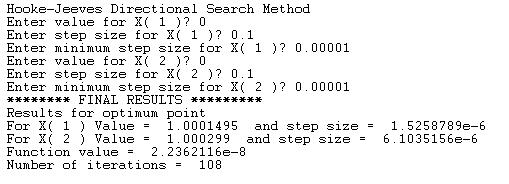
1. The coordinates of the minimum value.

2. The step size for each variable.

3. The minimum function value.

4. The number of iterations

The current code finds the minimum for the following function:

f(x1,x2) = 100 *(x1 ^ 2 - x2) ^ 2 + (1 - x1) ^ 2

Here is a sample session (the intermediate results have been edited out to shorten the session screen and to focus on the input and final output):

Here is the BASIC listing:

! Directional Search using Hooke and Jeeves method

OPTION TYPO
OPTION NOLET

DECLARE NUMERIC  MAX_VARS 
DECLARE NUMERIC  N, I, K
DECLARE NUMERIC  Iter, MaxIter
DECLARE NUMERIC  F, XX, Lambda, bOK
DECLARE NUMERIC  BestF, LastBestF, EPSF
DECLARE NUMERIC  bStop, bMadeAnyMove
DECLARE NUMERIC bTrue, bFalse

Dim X(1), Xnew(1)
Dim StepSize(1)
Dim MinStepSize(1)
Dim DeltaX(1)
Dim bMoved(1)

bTrue = 1
bFalse = 0

!---------------- Declare SUBs -------------------

SUB MyFx(X(), N, Res)
  Res = 100 * (X(1) ^ 2 - X(2)) ^ 2 + (1 - X(1)) ^ 2
  ! Res = X(1) - X(2) + 2 * X(1) ^ 2 + 2 * X(1) * X(2) + X(2) ^ 2
End SUB

SUB MyFxEx(N, X(), DeltaX(), Lambda, Res)
  LOCAL I
  Dim X2(1) 
  MAT ReDim X2(N)
  
  For I = 1 To N
    X2(I) = X(I) + Lambda * DeltaX(I)
  Next I
  
  CALL MyFx(X2, N, Res)
End SUB

Sub GetGradients(X(), N, Deriv(), DerivNorm)

  LOCAL XX, I, H, Fp, Fm

  DerivNorm = 0
  For I = 1 To N
    XX = X(I)
    H = 0.01
    If Abs(XX) > 1 Then H = H * XX
    X(I) = XX + H
    CALL MyFx(X, N, Fp)
    X(I) = XX - H
    CALL MyFx(X, N, Fm)
    X(I) = XX
    Deriv(I) = (Fp - Fm) / 2 / H
    DerivNorm = DerivNorm + Deriv(I) ^ 2
  Next I
  DerivNorm = Sqr(DerivNorm)
End Sub


SUB LinSearch_DirectSearch(X(), N, Lambda, DeltaX(), InitStep, MinStep, boolRes)

  LOCAL F1, F2
  
  CALL MyFxEx(N, X, DeltaX, Lambda, F1)
  
  Do
    CALL MyFxEx(N, X, DeltaX, Lambda + InitStep, F2)
    If F2 < F1 Then
      F1 = F2
      Lambda = Lambda + InitStep
    Else
      CALL MyFxEx(N, X, DeltaX, Lambda - InitStep, F2)
      If F2 < F1 Then
        F1 = F2
        Lambda = Lambda - InitStep
      Else
        ! reduce search step size
        InitStep = InitStep / 10
      End If
    End If
  Loop Until InitStep < MinStep
  
  boolRes = bTrue

End SUB

!---------------------------- MAIN PROGRAM --------------------

! Directional Search using Hooke and Jeeves method
  
MAX_VARS = 2
N = MAX_VARS

MAT REDIM X(MAX_VARS), Xnew(MAX_VARS)
MAT REDIM StepSize(MAX_VARS)
MAT REDIM MinStepSize(MAX_VARS)
MAT REDIM DeltaX(MAX_VARS)
MAT REDIM bMoved(MAX_VARS) 

PRINT "Hooke-Jeeves Directional Search Method"
For I = 1 To N
  PRINT "Enter value for X(";I;")";
  INPUT Xnew(I)
  PRINT "Enter step size for X(";I;")";
  INPUT StepSize(I)
  PRINT "Enter minimum step size for X(";I;")";
  INPUT MinStepSize(I)
Next I
  
! calculate and display function value at initial point
CALL MyFx(Xnew, N, BestF)
LastBestF = 100 * BestF + 100

Iter = 0
Do
  Iter = Iter + 1
  
  For I = 1 To N
    X(I) = Xnew(I)
  Next I
  
  For I = 1 To N
    bMoved(I) = bFalse
    Do
      XX = Xnew(I)
      Xnew(I) = XX + StepSize(I)
      CALL MyFx(Xnew, N, F)
      If F < BestF Then
        BestF = F
        bMoved(I) = bTrue
      Else
        Xnew(I) = XX - StepSize(I)
        CALL MyFx(Xnew, N, F)
        If F < BestF Then
          BestF = F
          bMoved(I) = bTrue
        Else
          Xnew(I) = XX
          Exit Do
        End If
      End If
    Loop
  Next I
  
  ! moved in any direction?
  bMadeAnyMove = bTrue
  For I = 1 To N
    If bMoved(I) = 0 Then
      bMadeAnyMove = bFalse
      Exit For
    End If
  Next I
  
  If bMadeAnyMove = 1 Then
    For I = 1 To N
      DeltaX(I) = Xnew(I) - X(I)
    Next I
    Lambda = 1
    CALL LinSearch_DirectSearch(X, N, Lambda, DeltaX, 0.1, 0.0001, bOK)
    If bOK = bTrue Then
      For I = 1 To N
        Xnew(I) = X(I) + Lambda * DeltaX(I)
      Next I
    End If
  End If
  CALL MyFx(Xnew, N, BestF)
  
  ! reduce the step size for the dimensions that had no moves
  For I = 1 To N
    If bMoved(I) = bFalse Then StepSize(I) = StepSize(I) / 2
  Next I
      
          
  ! show results
  Print "For iteration ";Iter
  For I = 1 To N
    Print "For X(";I;") Value = ";X(I);" and step size = ";StepSize(I)
  Next I
  Print

  ! remove next set of comments to pause between results
!  If Remainder(Iter, 8) = 0 And Iter > 0 Then
!    Print "Press any key to continue ...";
!    GET KEY K
!  End If      
      
  LastBestF = BestF
  
  bStop = bTrue
  For I = 1 To N
    If StepSize(I) >= MinStepSize(I) Then
      bStop = bFalse
      Exit For
    End If
  Next I
  
Loop Until bStop = bTrue

Print "******** FINAL RESULTS *********"
Print "Results for optimum point"
For I = 1 To N
  Print "For X(";I;") Value = ";X(I);" and step size = ";StepSize(I)
Next I
Print "Function value = ";BestF
Print "Number of iterations = ";Iter
END

The above listing has a set of commented statements that when uncommented will allow you to pause during the display of the intermediate results. The current code will display these intermediate results without pausing. For a large number of iterations, you will only see the data for the trailing iterations.

BACK