True BASIC Program to Find a Function Minimum

Using the Conjugate Gradient Method

by Namir Shammas

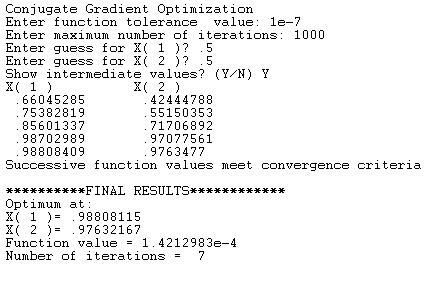
The following program calculates the minimum point of a multi-variable function using the Fletcher-Reeves conjugate gradient method.

The program prompts you to enter:

1. The function tolerance value.

2. The minimum number of iterations.

3. The initial guesses for the optimum coordinates.

The program also asks you whether or not you want to view the intermediate results.

The program displays the following final results:

1. The coordinates of the minimum value.

2. The minimum function value.

3. The number of iterations

The current code finds the minimum for the following function:

f(x1,x2) = 100 *(x1 ^ 2 - x2) ^ 2 + (1 - x1) ^ 2

Here is a sample session to solve for the optimum of the above function:

Here is the BASIC listing:

! Conjugate Gradient (Fletcher-Reeves) method

OPTION TYPO
OPTION NOLET

! Dim FTOL As Double
DECLARE NUMERIC MAX_VARS, boolRes
DECLARE NUMERIC  N, I, Iters, MaxIter, F, DFNorm, DFNormOld, Lambda, LastF, EPSF
DECLARE NUMERIC bTrue, bFalse

DECLARE STRING Ans$
Dim X(1), D(1), Dold(1)

bTrue = 1
bFalse = 0

!---------------- Declare SUBs -------------------

SUB MyFx(X(), N, Res)
  Res = 100 * (X(1) ^ 2 - X(2)) ^ 2 + (1 - X(1)) ^ 2
End SUB

SUB MyFxEx(N, X(), DeltaX(), Lambda, Res)
  LOCAL I
  Dim XX(1) 
  MAT ReDim XX(N)
  
  For I = 1 To N
    XX(I) = X(I) + Lambda * DeltaX(I)
  Next I
  
  CALL MyFx(XX, N, Res)
End SUB

Sub GetGradients(X(), N, Deriv(), DerivNorm)

  LOCAL XX, I, H, Fp, Fm

  DerivNorm = 0
  For I = 1 To N
    XX = X(I)
    H = 0.01
    If Abs(XX) > 1 Then H = H * XX
    X(I) = XX + H
    CALL MyFx(X, N, Fp)
    X(I) = XX - H
    CALL MyFx(X, N, Fm)
    X(I) = XX
    Deriv(I) = (Fp - Fm) / 2 / H
    DerivNorm = DerivNorm + Deriv(I) ^ 2
  Next I
  DerivNorm = Sqr(DerivNorm)
End Sub

SUB LinSearch_DirectSearch(X(), N, Lambda, DeltaX(), InitStep, MinStep, boolRes)

  LOCAL F1, F2
  
  CALL MyFxEx(N, X, DeltaX, Lambda, F1)
  
  Do
    CALL MyFxEx(N, X, DeltaX, Lambda + InitStep, F2)
    If F2 < F1 Then
      F1 = F2
      Lambda = Lambda + InitStep
    Else
      CALL MyFxEx(N, X, DeltaX, Lambda - InitStep, F2)
      If F2 < F1 Then
        F1 = F2
        Lambda = Lambda - InitStep
      Else
        ! reduce search step size
        InitStep = InitStep / 10
      End If
    End If
  Loop Until InitStep < MinStep
  
  boolRes = bTrue

End SUB

!---------------------------- MAIN PROGRAM --------------------

! Conjugate Gradient (Fletcher-Reeves) method

MAX_VARS = 2
MAT REDIM X(MAX_VARS), D(MAX_VARS), Dold(MAX_VARS)
N = MAX_VARS

! Input data
PRINT "Conjugate Gradient Optimization"
INPUT PROMPT "Enter function tolerance value: ": EPSF
INPUT PROMPT "Enter maximum number of iterations: ": MaxIter
For I = 1 to N
  PRINT "Enter guess for X(";I;")";
  INPUT X(I)
Next I  
INPUT PROMPT "Show intermediate values? (Y/N) ": Ans$
If UCASE$(Ans$[1:1]) = "Y" Then
  For I = 1 To N
      PRINT "X(";I;")",
  Next I
  PRINT
End If


! calculate and display function value at initial point
CALL MyFx(X, N, LastF)

CALL GetGradients(X, N, D, DFNorm)

Lambda = 0
CALL LinSearch_DirectSearch(X, N, Lambda, D, 0.1, 0.000001, boolRes)
If boolRes = 1 Then
  For I = 1 To N
    X(I) = X(I) + Lambda * D(I)
  Next I
Else
  PRINT "Failed linear search"
  STOP
End If

Iters = 1
Do
  Iters = Iters + 1
  If Iters > MaxIter Then
    PRINT "Reached maximum iterations limit"
    Exit Do
  End If
  DFNormOld = DFNorm
  For I = 1 To N
    Dold(I) = D(I) ! save old gradient
  Next I
  CALL GetGradients(X, N, D, DFNorm)
  For I = 1 To N
    D(I) = (DFNorm / DFNormOld) ^ 2 * Dold(I) - D(I)
  Next I
  If DFNorm <= EPSF Then
    PRINT "Gradient norm meets convergence criteria"
    Exit Do
  End If

  Lambda = 1
  CALL LinSearch_DirectSearch(X, N, Lambda, D, 0.1, 0.000001, boolRes)
  If boolRes = 1 Then
    For I = 1 To N
      X(I) = X(I) + Lambda * D(I)
    Next I
    CALL MyFx(X, N, F)
    If Abs(F - LastF) < EPSF Then
      PRINT "Successive function values meet convergence criteria"
      Exit Do
    Else
      LastF = F
    End If
    
  Else
    PRINT "Failed linear search",
    Exit Do
  End If
  If UCASE$(Ans$[1:1]) = "Y" Then
    For I = 1 To N
      PRINT X(I),
    Next I
  PRINT
  End If
Loop

PRINT
PRINT "**********FINAL RESULTS************"
PRINT "Optimum at:"
For I = 1 To N
  PRINT "X(";I;")=";X(I)
Next I
PRINT "Function value ="; LastF
PRINT "Number of iterations = ";Iters  
END

BACK